Exemplo De Equação Do 2 Grau Delta Maior Que Zero – Exemplo De Equação Do 2º Grau Delta Maior Que Zero: o estudo de equações quadráticas com discriminante positivo revela um universo rico em soluções e aplicações práticas. Compreender o significado de um delta maior que zero é fundamental para desvendar as raízes reais e distintas dessas equações, abrindo portas para a resolução de problemas em diversas áreas, desde a física até a engenharia.
Neste estudo, exploraremos os métodos de resolução, as interpretações geométricas e a modelagem matemática associada a esse tipo de equação, fornecendo exemplos concretos e aprofundando o entendimento deste tópico crucial da matemática.
A forma geral da equação do segundo grau é ax² + bx + c = 0, onde ‘a’, ‘b’ e ‘c’ são coeficientes reais, com ‘a’ diferente de zero. O discriminante, ou delta (Δ), é calculado por Δ = b²
-4ac. Quando Δ > 0, a equação possui duas raízes reais e distintas, calculadas pela fórmula de Bhaskara: x = (-b ± √Δ) / 2a.
A fatoração também pode ser utilizada como método de resolução em alguns casos, oferecendo uma alternativa à fórmula de Bhaskara. A interpretação geométrica dessas equações envolve uma parábola que intercepta o eixo x em dois pontos distintos, correspondentes às raízes encontradas.
Equação do 2º Grau: Quando Delta é Maior que Zero: Exemplo De Equação Do 2 Grau Delta Maior Que Zero
A equação do 2º grau é uma ferramenta matemática poderosa com diversas aplicações em áreas como física, engenharia e economia. Compreender seu comportamento, especialmente quando o discriminante (delta) é maior que zero, é fundamental para resolver problemas práticos e interpretar resultados.
Introdução à Equação do 2º Grau, Exemplo De Equação Do 2 Grau Delta Maior Que Zero

A forma geral da equação do 2º grau é representada por: ax² + bx + c = 0, onde ‘a’, ‘b’, e ‘c’ são coeficientes reais, com ‘a’ diferente de zero. O coeficiente ‘a’ determina a concavidade da parábola (se abre para cima ou para baixo), ‘b’ influencia a posição do vértice e ‘c’ representa o ponto de intersecção com o eixo y.
O discriminante, ou delta (Δ), é definido pela fórmula: Δ = b². Este valor determina a natureza das raízes da equação.
-4ac
Delta Maior que Zero: Raízes Reais e Diferentes
Quando o delta (Δ) é maior que zero (Δ > 0), a equação do 2º grau possui duas raízes reais e distintas. Isso significa que a parábola intercepta o eixo x em dois pontos diferentes. Para encontrar essas raízes, utilizamos a fórmula de Bhaskara:
x = (-b ± √Δ) / 2a
onde x1 e x2 representam as duas raízes.
| Equação | a | b | c | Delta | Raízes (x1, x2) |
|---|---|---|---|---|---|
| x² – 5x + 6 = 0 | 1 | -5 | 6 | 1 | (2, 3) |
| 2x² + 3x – 2 = 0 | 2 | 3 | -2 | 25 | (0.5, -2) |
Métodos de Resolução para Delta > 0
A fórmula de Bhaskara é um método geral para encontrar as raízes de uma equação do 2º grau, independentemente do valor de delta. A fatoração, por outro lado, é um método mais direto que pode ser aplicado quando a equação pode ser facilmente decomposta em fatores. A fatoração geralmente é mais rápida quando aplicável, enquanto a fórmula de Bhaskara sempre funciona.
Exemplo utilizando a fórmula de Bhaskara para a equação x²
-5x + 6 = 0:
Δ = (-5)²
-4
– 1
– 6 = 1
x1 = (5 + √1) / 2 = 3
x2 = (5 – √1) / 2 = 2
Exemplo de fatoração para a equação x²
-5x + 6 = 0:
| Passo | Descrição do Passo | Expressão Algébrica | Resultado |
|---|---|---|---|
| 1 | Encontrar dois números que somados resultem em -5 e multiplicados resultem em 6. | (x – 2)(x – 3) = 0 | -2 e -3 |
| 2 | Igualar cada fator a zero e resolver para x. | x – 2 = 0 e x – 3 = 0 | x = 2 e x = 3 |
Aplicações da Equação do 2º Grau com Delta > 0
Um exemplo prático: Um projétil é lançado verticalmente para cima com velocidade inicial de 20 m/s. Sua altura (h) em metros após t segundos é dada por h(t) = -5t² + 20t. Em que instantes o projétil estará a 15 metros de altura? Para resolver, igualamos a equação a 15: -5t² + 20t =
15. Simplificando, temos: -5t² + 20t – 15 =
0.
Resolvendo esta equação do 2º grau (dividindo por -5 para simplificar: t² -4t + 3 = 0), encontramos dois instantes (t1 e t2) em que o projétil atinge 15 metros de altura. Usando a fórmula de Bhaskara ou fatoração, encontramos t1 = 1 segundo e t2 = 3 segundos.
Interpretação Geométrica
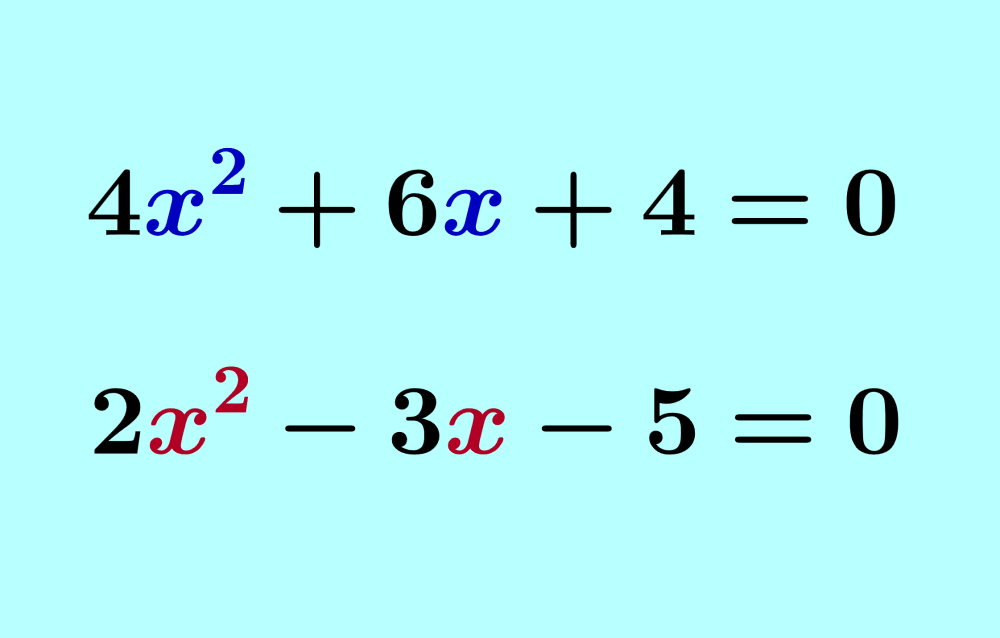
Geometricamente, quando Δ > 0, a parábola representativa da equação do 2º grau intercepta o eixo x em dois pontos distintos, que são as raízes da equação. O vértice da parábola, ponto de máxima ou mínima altura, situa-se entre esses dois pontos de intersecção. A parábola é simétrica em relação a uma reta vertical que passa pelo vértice. A concavidade da parábola é determinada pelo sinal do coeficiente ‘a’: se ‘a’ > 0, a parábola abre para cima; se ‘a’ < 0, a parábola abre para baixo.
Exemplos Adicionais e Discussão
- Equação: 3x²
-7x + 2 = 0; a = 3, b = -7, c = 2; Δ = 25; Raízes: x1 = 2, x2 = 1/3 - Equação: -x² + 4x – 3 = 0; a = -1, b = 4, c = -3; Δ = 4; Raízes: x1 = 3, x2 = 1
- Equação: x²
-6x + 5 = 0; a = 1, b = -6, c = 5; Δ = 16; Raízes: x1 = 5, x2 = 1

